from the IAPPP Communications, Spring 1994 issue
R. E. Wilson
Astronomy Department
211 Space Sciences Building
University of Florida
Gainesville, Florida 32611 USA
Received: 6 January 1994; Revised: 2 March 1994
(some updates by DCT on the web version)
This review concerns the interpretive side of the subject that is, how astrophysically meaningful numbers are extracted from observed light curves. One aim is to inform potential users about the existence of various modeling programs, so that the programs may be used directly by observers. Another will be to put today's light curve fitting procedures in perspective, by comparison with intuitive methods and even with old graphical methods. Along the way, we shall see how to go from observed light (and radial velocity) curves to astrophysical quantities the overall goal of observing.
Examine typical eclipsing binary light curves and compare them with other kinds of binary star observations, such as radial velocity curves and visual binary data. It is not so obvious from casual inspection which kind of observation has more harmonic content (carries more information), or which kind would be chosen by an astronomically naive judge as physically more complicated. Just a little thought settles the second issue, however. For spectroscopic and visual binaries, the essential phenomenon is one of point sources moving on simple curves, usually with no significant interaction. There are difficulties which require experience, but mainly they are in the observations, while the models are simple. The situation is reversed with light curves the observations are typically clean and periodic and there are only relatively minor analogies to the line blending and profile effects of radial velocities or the subjective effects of visual binary observing (which have been eliminated recently by interferometric and speckle methods of observing). Not only are the light curves relatively accurate and reproducible, but they can be obtained with much less effort, and therefore are more plentiful. Typical sets of published spectroscopic binary observations contain tens of data points, while light curves contain hundreds or even thousands. There are problems with the light curves of some binaries, but typically they are met less often and are on a much smaller scale than those of the other cases.
Ah, but then there are the models. Now instead of points moving on ellipses we have tidally and rotationally distorted stars with their inner facing sides heated by the companion's radiation. We have brightness variation over the surfaces due , to variation in surface gravity, and we have limb darkening. We have not just geometry, but thermal radiation effects, as the light curve is a superposition of local radiation curves, and not just those of black bodies, but the much more intricate radiation of real stars. There may be a complication due to the light of a third star, and we may have magnetic star spot activity on a scale much greater than does the sun, and sometimes even a hot spot due to impact of an accretion stream. Finally there are the eclipses, which are both the most useful and computationally difficult feature of the overall problem. However, all of these difficulties are problems for the model makers and programmers. Extraction of astrophysical information from a light curve does not require one to deal with such things, because the required programs already exist, so let us move on to solving light curves.
The practice of obtaining information about a binary from its light curve is variously known as solving, or fitting, or interpreting the light curve. To some, these terms may conjure up different mental images. "Solving" sounds like a very formal procedure, "fitting" like trial and error, and "interpreting" like sitting back in a rocking chair and offering opinions. In practice, solving and fitting are treated essentially as synonyms, as is interpreting, except that the identification of unusual features might be included within interpreting. Regardless of the word used, the idea is to estimate values of physical and geometrical quantities (parameters) such as the mass ratio of the two stars, their sizes, and their relative luminosities.
Now for a key question could an amateur observer do this? On the one hand, it is not so unusual for a professional to "get it wrong", and a significant fraction of published papers in this area contain no new data, but only improve on previous (perhaps inaccurate) solutions. If questionable solutions can be found by professionals, what chance has the amateur? Also, an amateur ordinarily would have no opportunity to learn from an experienced person, and certainly not to take a course in the subject. On the other hand, light curve fitting can be learned by an imaginative person, and all the hard computing is done by a big program, so why not? Collaboration between amateurs and professionals now is fairly common, and is an excellent option. Publication of an observed light curve without solving it is all right, but inclusion of a solution is more satisfying and takes only modest space in a paper. The required computing facility consists of no more than a fairly good personal computer, of the type now found in many households, and a compiler (usually FORTRAN). Of course, one might have a few collaborations and then strike out alone. The only bad option is not to publish those valuable light curves.
The basic type of analysis for measurement of binaries, going back perhaps 90 years, is the generic light curve - radial velocity curve analysis. In a beginning course, astronomy students (are supposed to) learn what can be found from various combinations of light and velocity curves, such as a light curve at some effective observational wavelength and velocity curves for both stars, or a light curve only, or a light curve and one velocity curve, etc. While there is a little overlap in the areas of information provided by light and velocity curves, they mainly give quite different information, so that neither can replace the other. Orbital period, eccentricity and orientation, and sometimes the mass ratio can be found from both sources (see Sec. II for a brief explanation of photometric mass ratios). The standard complete set is a light curve of the whole system and the radial velocity curves of both binary components. Somewhat better is to have multi-bandpass light curves (two or more effective wavelengths), but the irreducible minimum for essential measurement is one light curve and both velocity curves. (footnote 1) The reason for this can be seen in thought experiments. Imagine a binary star model made of phosphorescent wooden stars plus a motor for orbital motion and observe its light curve with a photometer from a large distance. Now double the size of everything in the model, including the orbit, and observe again. Although the absolute amount of light received will now be larger, the new light curve can be re-scaled to coincide with the first one. Since changing the observer-model distance or the brightness of the paint could achieve the same re-scaling, one shape of light curve corresponds to an infinity of size-distance-surface brightness combinations. This demonstrates that a light curve cannot tell us absolute dimensions, either of the stars or of the orbit. Of course, if one happened to know the distance and surface brightnesses (perhaps through cluster membership and spectral types, when dealing with real stars), one could estimate the absolute sizes. However that can be done just as well for a single star, so nothing about the form of a light curve tells about absolute size.
What does a light curve tell? Try changing the size of one or both wooden stars while keeping the orbits the same. A little mental imagery shows immediately that the circumstances of eclipses will change, so that the light curve must change in form. An eclipse might change from total to partial or vice versa, eclipses might occupy a larger or smaller part of the orbital cycle, and eclipse depths and shapes should change. Obviously a light curve can tell us about relative star sizes relative to the orbit size and relative to each other. Further thought experiments will show that a light curve can tell us star shapes and various kinds of surface brightness and orientation information.
A velocity curve tells little or nothing about star size or shape because the stars essentially act as geometrical points in producing a velocity curve. Viewed simply, what we measure is a Doppler shift averaged over the unresolved stellar disk, and that average is almost the same as that of the star as a whole. However a velocity curve has the great merit of measuring certain geometrical properties in terms of absolute length not just length ratios but real lengths in kilometers. This is evident from the units of radial velocity, such as kilometers per second. Obviously, if we know the line of sight velocity at each moment of time, we can keep track of where the object is along the line of sight, relative to some arbitrary starting point. So light curves can provide a picture of the binary with an unknown scale, while radial velocity curves can provide the absolute. scale, but no picture. Velocity curves of both stars are needed to complete the scaling information, although radial velocities for just one of the stars give useful, but incomplete, information.
A natural distinction is between absolute and relative orbits, because the former relate to radial velocity curves while the latter relate to light curves. Radial velocities can be referenced to the binary system center of mass, which has a constant radial velocity (unless we are dealing with a multiple system rather than only a binary system). Furthermore, the velocity curves are observed separately for the two stars, in contrast to the light curve, which is observed only in their blended light. One can say that the system is resolved in radial velocity but unresolved in position. Accordingly, the separate velocity curves allow us to determine the changing line of sight star locations with respect to the center of mass. Thus a natural concept for velocity curves is the absolute orbit, which is the orbit of a star with respect to the center of mass. A light curve contains information about the changing location each star with respect to the other, which is called a relative orbit. There is a relative orbit for each star, but the two relative orbits have, of course, the same size and shape. The absolute orbits have the same shape, but the ratio of their sizes is the inverse of the mass ratio, so the more massive star has the smaller orbit. We can think of a relative orbit as the sum of the two absolute orbits.
A text book treatment could be as follows. Writing i for orbital inclination and a's for orbital semi-major axis lengths, the respective radial velocity curves give a, sin i and a2 sin i for stars 1 and 2, and thus a sin i, where a = a, + a2. Thus, if both velocity curves have been observed, we have the orbit dimensions, both absolute (a,, aZ) and relative (a), but including an unknown projection factor of sin i. A suitable light curve can give relative radii, r, = R,/a and r2= R2/a, as well as sin i, but nothing absolute neither R, nor R2 nor a. If we put light and velocity information together we have absolute R, , R2, and a in kilometers, uncomplicated by sin i. Notice that none of this requires any knowledge of the observer-to-binary distance since Doppler-determined velocities and percentage brightness changes are unaffected by distance, given that the basic observations can be made with suitable accuracy.
In the late 1960's, fast automatic computers built with integrated circuits began to be widely available. While they were slow compared to today's machines, the speed increase over their (separate transistor) immediate predecessors was enormous a factor of perhaps 200. This made numerical light curve models practicable. Two main advances were the order of the day and, while most of the new computer models incorporated both advances, not all did. The really obvious improvement was to scrap rectification and compute light curves directly. That is, to put mutual heating and tidal effects, etc. into the theory rather than trying to take them out of the observations. The other improvement was to "get physical". Direct computation can be done for ellipsoids (Wood 1971), and has many important benefits compared to rectification, but why not work with the level surfaces of constant potential energy which physical theory predicts for a star in hydrostatic equilibrium? In brief, star surfaces coincide with surfaces of constant potential energy per unit mass, and local gravity is inversely proportional to the spacing of the surfaces. (For background reading on this subject, see Wilson 1974). The fundamental concept from which the rest has followed was Z. Kopal's idea of computing light curves based on the geometry of equipotential surfaces. Many important thoughts are contained in his book "Close Binary Systems" (Kopal 1959) and the thoughts were there, waiting for fast computers to arrive. In the interim, Kopal investigated methods of correcting spherical model light curves so as to produce, as nearly as possible, light curves of equipotential models. That work has not been used to any significant extent to analyze observations of real binaries and it is no longer needed, given the existence of fast computers and direct utilization of the equipotentials, but the mathematical cleverness which went into it is impressive. Notice that the issue of which radius best represents the size of a non-spherical star is avoided entirely when we specify the surface by a value of potential energy.
Not only are equipotential models directly physical and able to avoid rectification, but they implicitly contain the essential morphology of close binaries and can use it to constrain solutions. Here are two intimately related ideas morphology and constrained solutions which permeate modern light curve work. With regard to morphology, Kuiper (1941) published a paper on P Lyrae in which he freely made use of concepts of limiting surfaces which did not become well established until almost two decades later. Kuiper did not use all the names we use today for morphological types (detached, semi-detached, and overcontact), but this was a landmark paper which included equipotential diagrams, and he did call P Lyrae overcontact (although that is not the present view of P Lyrae's type).
The type names, as a coherent set, were introduced by Kopal (1954; 1959). The physics of morphological types is embodied in special lobes which limit the sizes of the two stars and the outer contact surface. This limits the size of the binary as a whole. Assume circular orbits and synchronous rotation, in which case the rotation period will be the same as the orbit period. The idea is that there must be a null point of effective gravity between the two stars, where the two gravities plus centrifugal force add to zero in a coordinate frame which rotates with the system. So if we imagine one of the stars increasing in size (and continuing to co-rotate), it will follow a succession of equipotentials and eventually reach one which includes the effective gravity null point. It then begins to expel surface gas out through a small nozzle where gas pressure is not balanced by gravity. The loss of material prevents the star from becoming any larger, so it accurately conforms to the size and shape of that particular equipotential, which is known as its Roche lobe. Of course, the other star also has a Roche lobe. A binary with one star in contact with its lobe and the other detached is called a semi-detached binary (see U Sagittae in Figure 1), while if both stars lie within their lobes the binary is called detached. An overcontact binary is one in which both stars exceed their Roche lobes and have a common envelope, so there are not two separate surfaces but only ones (Figure 2 shows the overcontact binary RR Centauri.) That surface cannot be arbitrarily far out, but is limited at the system's outer contact surface, where there is another effective gravity null point and gas can escape from the binary system. This set completes the list of morphological types expected in the synchronous-circular case, but if rotation is non-synchronous there can be one more type, that of double contact (Wilson 1979; Wilson, Van Hamme and Pettera 1985; Wilson 1994), in which both stars accurately fill their limiting lobes.
 |
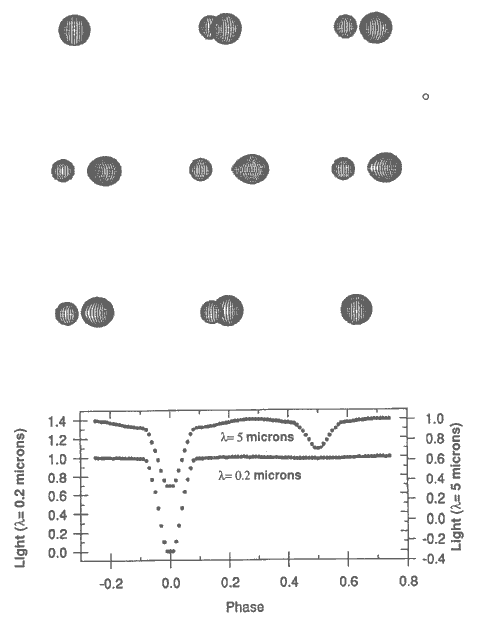| FIGURE 1. Computer generated pictures of U Sagittae and computed light curves at 5.0 and 0.2 microns (infrared and ultraviolet, respectively). Note that the secondary star is reasonably prominent in the IR but not in the UV. The small circle in the upper right margin represents the Sun on the same scale. |
 |
| FIGURE 2. The overcontact binary RR Centauri. The surface of the common envelope lies above the Roche lobes, at a single potential energy. RR Cen belongs to the W UMa class of binaries. The small circle in the upper right margin represents the Sun on the same scale. |
The main reason for this brief discussion of morphological types is that an important class of constraints on light curve solutions is based on morphology. Suppose something is known about possible solutions, such as that one of the stars accurately fills its limiting lobe. Evidence for this circumstance can come from several kinds of observations unrelated to light curves. In the interest of simplicity, consider only the synchronously rotating, circular orbit case. Since the relative lobe size, and thus now star size, depends uniquely on the mass ratio, one should not try to estimate the star size and mass ratio independently. Although perhaps neither quantity is known with great accuracy, a value for one implies a definite value for the other. This extra information can be used appropriately if the computer program is able to constrain solutions so as to allow only compatible combinations of star size and mass ratio, as can the WD program (Wilson 1979). The constraint thus reduces the parameter list by one and rules out an entire dimension of incorrect solutions. In effect, information from a source or sources external to the light curves is used to improve the light curve solutions. Application of this constraint allows determination of mass ratios from light curves, and these are called photometric mass ratios (viz. Wilson 1994 for a more detailed explanation). Other examples of solution constraints are covered in Wilson (1988).
The essence of the conceptual link between binary star morphology and modeling constraints is that a light curve program can be constructed so as to produce only a particular morphology, if that is the user's wish. For example, one can vary the mass ratio and maintain a semi-detached configuration without continually re- calculating the size of the lobe-filling star, because the program can be asked to do that automatically. It can do so whether it is computing synthesized observations from parameters (direct problem), or solving for parameters from observations (inverse problem). The WD program identifies various constraints with eight different modes in which it can be run, as described in Wilson (1992; 1993).
An overview of the history of light curve models is contained in Wilson (1994). Fortunately, interests and emphases have varied greatly among the developers of physical models, with the result that many productive lines of modeling have followed from a variety of original ideas. This is a healthy situation, in which various persons have emphasized different areas of the overall problem. While a given program may not be able to handle certain kinds of cases, the ones it can do might be especially accurate or otherwise well done. A listing of the major papers would be unduly long, while a listing of individual names would fail to recognize notable collaborations. The following alphabetical list of names and combinations is intended as a compromise: E. Berthier (1975); D.H. Bradstreet (1993); E. Budding (1977); G.V. Cochrane (1970); J.A. Eaton (1975); P.B. Etzel (1993); P.D. Hendry and S.W. Mochnacki (1992); G. Hill (1979); Hill and J.B. Hutchings (1970); Hill and S.M. Rucinski (1993); J. Kallrath (1993); Kallrath and A.P. Linnell (1987); Linnell (1984); L.B. Lucy (1968); H. Mauder (1972); Mochnacki and N.A. Doughty (1972); T. Nagy (1974) and L. Binnendijk (1977) (footnote 2); B . Nelson and W. Davis (1972); A. Peraiah (1970); Rucinski (1973); R.E. Wilson (1979); Wilson and E.J. Devinney (1971); D. B . Wood (1971). The reference given for each author or pair of authors is not necessarily the one most representative of their contributions, but more complete references are given in Wilson (1994).
The list includes some persons who have been interested in parameter estimation rather than model development. Among the model developers, the focus may be mainly on accurate computation (Linnell; Hendry and Mochnacki), on computing speed for special cases (Budding; Etzel; Wood), on generality, or applicability to a wide variety of binaries (Wilson), or another area. Some of the resulting programs are available for the asking or for a modest charge, while others are not. The originators, whose addresses are to be found in the membership lists of the major astronomical societies, can be contacted in this regard. Also important are contributions on sub-computations, such as radiation by stellar atmospheres (Linnell 1991; Milone, Stagg, and Kurucz 1992) and limb darkening laws (e.g. Al-Naimiy 1978; Diaz-Cordoves and Gimenez 1992; Klinglesmith and Sobieski 1970; Van Hamme 1994).
There are other persons (not listed) whose objective was simply to produce a working program patterned after an existing one. Indeed, there has been some writing of new programs without significant innovation, typically so as to have a program whose content is completely known to the programmer-user. When the emphasis is on results, it can be effective to write a relatively simple program which just gets the job done. With X-ray binaries, for example, one of the stars is essentially a point (a black hole, neutron star, or white dwarf), and this renders eclipse computations trivial or unnecessary. The circular orbit simplification also applies to some X-Ray binaries. However, workers in such areas should be aware of potentially important capabilities present in some of the more general modeling programs. For example, suppose compact object is in eccentric orbit around a supergiant star, as with the neutron stars in HD 77581 (see Figure 3) and HD 153919. Because the eccentrically orbiting neutron stars are not very far outside their companions, the orbital motions necessarily drive complicated non-radial oscillations of the supergiants. The variation of such a star's figure cannot be followed well by a simple program which invokes static equipotentials, yet a more. general program may more nearly follow the real variation (e.g. Wilson 1979; Wilson and Terrell 1994).
It was mentioned in the Introduction that the average Doppler shift over a stellar disk is almost the same as that of the star as a whole, but there can be a significant difference (proximity effect) where tides or reflection are important. This is especially true for a star which is much more massive than its companion, because orbital velocities are then small and proximity effects can be relatively appreciable. Light curve models are now often used to compute velocities properly averaged over the surface. Once one has written a light curve program, only minor additional steps are needed to compute integrated radial velocities, as well as other observable quantities, such as polarization variables (Wilson 1993; Wilson and Liou 1993). Some discussion and further references are in Wilson (1994).
Your working apparatus is a binary star model, as embodied in one of the existing programs, and a personal computer or workstation. It is best to obtain the program from its originator rather than from another user. This should assure you of having the latest version, which should be the most developed and free of bugs. Your first assignment is
 |
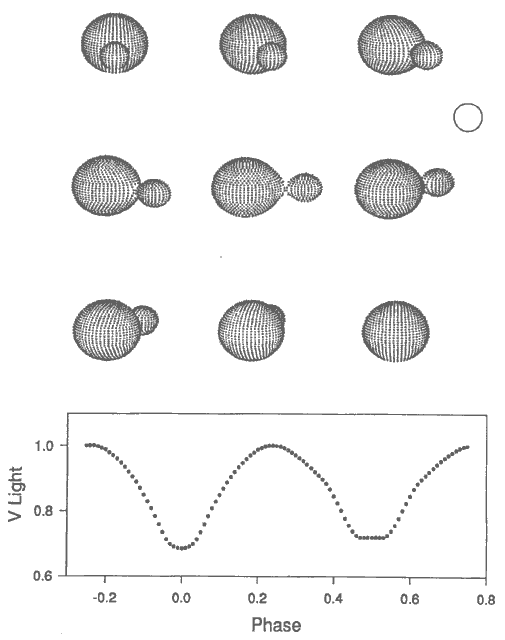
| FIGURE 3. The blue supergiant - neutron star X-ray binary GP Velorum or HD 77581 to optical observers and as Vela X-1 to X-ray observers. Notice the proximity of the components, which results in large and complicated tides. The sun's size is indicated by a small circle in the upper right; the neutron star's size is greatly exaggerated for clarity. |
to contact the originator and pry a copy loose (hint: you are unlikely to meet in the supermarket line, so do a little detective work). Willingness to provide programs and cost (perhaps free) vary among modelers, so you should be prepared to make a case for being a serious user.
The model is characterized by a number of parameters, such as the mass ratio (m2/m,) and the orbital inclination (i). There may be something like 15 to 30 such parameters, depending on which model you use, and your problem is to come up with estimates for their numerical values. We begin with a principle which is so basic and obvious that some persons lose sight of it among the details of a solution. It is as fundamental in parameter fitting as is the "Fundamental Theorem of Algebra" in solving simultaneous equations (there cannot be a unique solution unless the number of unknowns matches the number of equations). It might be called the Individuality Principle, and it is just this: A parameter can be determined only if its variation affects observable quantities in a different way than does the variation of any other parameter. In the language of statistics, two parameters which affect the observables in exactly the same way are said to be completely correlated. Of course, the "observable quantities" are those actually at our disposal. There is no help to our solution provided by unavailable data.
An ideal situation for determining a parameter is one in which it affects the observations in a unique way, thoroughly differently from any other parameter of interest, and thus is completely uncorrelated with the other parameters. However that seldom is found most pairs of parameters are partially correlated, which means that there is some similarity in the ways they affect data. Now what does this have to do
 |
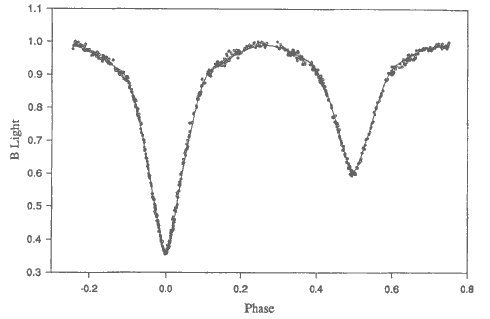| FIGURE 4. A good B light curve of TT Aurigae observed by Wachmann, Popper, and Clausen (1986) and fitted by Terrell (1991). Agreement between model and observations is not perfect, but make no apologies if you do as well as this. |
The maxim seems so obvious, so why even mention it? Because the advice sometimes is put aside even by professionals, when enthusiasm overruns common sense. It is astonishing to see someone who would never try to read temperature directly from a pressure gauge actually attempt to find the temperatures of both stars of a binary from a light curve, where the Tl, T2 correlation is almost perfect. So spend some time in thought experiments. Vary parameters in your mind and ask what should be the effects on the light curve. Then run a light curve program to see if you were right. Fit many light curves by trial and error, with liberal use of graphs. If the machine produces a counter- intuitive result, think about it until you understand. That is the real way to learn.
You will not be able to find meaningful estimates for all parameters from your light curves, but you will need to insert some values, so what is to do? The basic options are to adopt astrophysically reasonable numbers or numbers derived from some other kind of observations of your binary. There are no hard and fast rules here common sense is the only common thread. For example, suppose you need a number for the mass ratio and have decided that your light curves cannot tell you this number because the mass ratio is correlated with other quantities. Of course, you first look for double-lined radial velocity curves, which are the ordinary source of mass ratio information. These may or may not be available and they may be good or bad. If velocities are not available at all, you will have to assume the mass ratio from the spectral and luminosity types of your stars. If they are available but extremely noisy, or you suspect serious systematic errors in the velocities, you still may want to use the spectral and luminosity types, or you may want to re-think the possibility of at least setting limits on the mass ratio via light curve fitting experiments. In the end, you might arrive at a mass ratio based on the confluence of several kinds of considerations, perhaps some not even mentioned here.
Up to this point we have not imagined the actual process of fitting light curves as it would take place at a personal computer. The process consists of two parts, a subjective stage in which we use intuition and numerical experiments to get reasonably close, and a mainly objective stage in which a programmed algorithm leads iteratively to our final solution. Practical tips for carrying out both stages are to be found in the: documentation provided with some of the programs (e.g. Wilson 1992). The objective criterion for best fit used by almost everyone is the least squares criterion, which is that the sum of the squares of the weighted residuals is as small as possible. That is, the parameters of the problem are adjusted to produce a minimum of that sum of squares. A residual is just the difference between an observed quantity and its computed value, according to our adopted model. The subject of weighting is somewhat intricate and would lead us astray from our main discussion, but some of the computer programs take care of weighting automatically (viz. Wilson 1979).
Now what is actually supposed to happen in the progress of a solution? Before. there were personal computers we would have to make graphs by hand, so as to compare the computed (theoretical) and observed light curves, which was an enormous amount of work. Happily, the personal computer now can do that for us, if aided by an appropriate software package. We have come a long way from the old days, thanks to personal computers, workstations, laser printers, and plotting software. However most light curve programs do not make light curve plots or binary system pictures because they are intended to be portable (i.e. to work on a wide variety of computers). While their source languages, such as FORTRAN, are portable, plot routines are machine- specific on today's hardware. The information to make pictures is in the machine, but some (minor) programming is needed to get it to the local plotter. For this reason, a few programs have been written which are mainly intended to make pictures of binaries and plots of their light curves. These programs have restricted portability, although the restriction may not be very severe. For example, such a package may work on most or all IBM compatible personal computers.
One very convenient package is D.H. Bradstreet's (1993) Binary Maker, which shows light and radial velocity curves together with pictures of a binary, and even has a zoom feature, by which one can expand and contract the binary star image. Another is D. Terrell's (1992) Wilson-Devinney User Interface, which can picture non- synchronously rotating and eccentric orbit binaries and, in general, enable a PC user to work with the WD program interactively and to produce screen plots and pictures. Pictures and light curves also are shown in an overview article (Wilson 1974) and in the book Binary Stars: A Pictorial Atlas (Terrell, Mukherjee, and Wilson 1992).
Once you have a plot program it will be easy to check your intuition, so do many experiments. You also should inspect the distribution of surface elements (dots), which is characteristic of each particular program, so as to get a feeling for circumstances in which the program might begin to lose accuracy. Ordinarily an essentially uniform sprinkling of elements over the surface is desirable, and some coordinate systems or element-generating schemes achieve this better than others. However, to keep all this in perspective, remember that the really essential plot capability is the one which compares observed and computed light curves. The star picture capability is nice but can be replaced by good mental imagery for most purposes.
Now for some intuition. For the most part, each person needs to carry out personally tailored thought experiments, but we can start with a few to show the basic idea. Given a light curve or curves (preferably they should be multi-bandpass), begin by seeking an overview of the situation. This comes prior to any computation, whether assisted by screen graphics or not. Inspect the observed light curve or curves, note the main characteristics, and try to picture a plausible corresponding binary configuration. This requires some familiarity with the main phenomena which affect light curves. Such familiarity can be developed by computational experiments, but let us suppose you have done that for the generic case and are now faced with real observations of an actual binary.
What should you have learned from your experiments to bring to bear on a real problem? Well, you should have made a mental connection between tidal distortions and the double-humped variation they produce, which sometimes is called ellipsoidal or ellipticity variation. Tides stretch the stars into ovals, with the long axes along the line of star centers. The system is bright when we see the largest areas (broadside, or about midway between eclipses) and faint around the conjunctions (when we expect the eclipses). There also is a surface brightness effect, due to gravity brightening, which enhances the geometrically produced variation and is called photometric ellipticity. Overall, the light changes follow a curve which is something like a double cosine wave (i.e. the light goes through a cosine-like variation twice per orbit), but not with quite the shape of a cosine. Superposed on this may be a reflection effect, or really two reflection effects, one from each star. Here the heated cap on the inner facing side of each star tends to produce a once-per-orbit brightening when it is most directly in view, which is at only one of the conjunctions. As with the tidal effect, reflection variation is (very) roughly sinusoidal, but with only one "cosine" cycle per orbit. Notice that the main tidal distortion effects of the two stars are effectively in phase because the star figures have approximate front-to-back symmetry and thus look roughly the same from the two ends.
The tidal effects therefore primarily accentuate one another, while the two reflection variations are 180° out of phase and will partly cancel. Thus we expect (with other things being equal) an obvious reflection variation mainly when stars of very different temperature are paired. (Why it is temperature rather than luminosity which matters is a thought problem left to the reader.) So the combined reflection effect of the two stars will be most noticeable as a brightening of the "shoulders" of one eclipse, and that will be the eclipse of the lower temperature star. During the eclipse itself, of course, the reflection cap may be out of view. An unusual reflection effect is seen in V 1647 Sagittarii (Figure 5), which has an eccentric orbit and shows a reflection peak only near periastron where heating is greatest.
While there may be a natural psychological tendency to focus on eclipses when sizing up a light curve, the tidal and reflection effects are important and need to be considered together with the eclipses at all stages of the fitting process, including the preliminary rough estimates. One should realize that an enormous tide can be present on a star, with almost no evidence of it in the light curve. In Algol, for example, the dim secondary star is drawn out into a teardrop shape, but contributes something like only two percent of the system light, so its big tide hardly affects the light curve at all. Large reflection effects also can appear only subtly in a light curve. AG Persei consists of a pair of very hot stars with big individual reflection effects, but the two reflection effects are nearly equal and largely cancel, at least to casual inspection. The lesson is that one has to keep the entire binary configuration in mind in thinking about the various interacting effects.
What can be inferred about a binary from inspection of tidal and reflection variations? The tidal effect naturally is large for stars which are big compared to the orbital separation, and is especially large for overcontact systems, so it should essentially be a measure of star size, relative to the orbit. However, think about this. Stars which are big compared to the orbit tend to produce eclipses of long duration (i.e. wide in phase), so eclipse duration would seem to tell all we need to know about star size, leaving tides a redundant source of information. However eclipse duration drops faster with reduced orbital inclination than does tidal variation (i= 90° for an edge-on orbit). For example, diminish the inclination of a model overcontact binary to 60° and the eclipses will nearly disappear, while the tidal amplitude still will be about 70% as large as for 90°.
There are other things to remember, such as that a low temperature star has reduced ellipsoidal amplitude due to the relatively small gravity brightening effect of a convective envelope. Therefore only a few examples of this sort can be given, and many numerical experiments will be needed to instill a feeling for effects of tidal distortion. However, with the help of a screen graphics program they are fun to do, especially against a background of real observations. Similar remarks can be made about the reflection effect.
Finally it is time to think about eclipses. The facts are easy to tell, but why they are true would demand a long discourse. Fortunately, all make intuitive sense, so formal derivations are not needed for overview purposes. Do not regard them as rigorous laws, but as approximately correct rules which connect observed light curves with models, and thus allow one to guess parameters. That is, most items really require qualifiers, such as "disregarding limb darkening effects", or "neglecting proximity effects", etc. Light curves are assumed to be plotted in observed flux, not astronomical magnitude.
 |
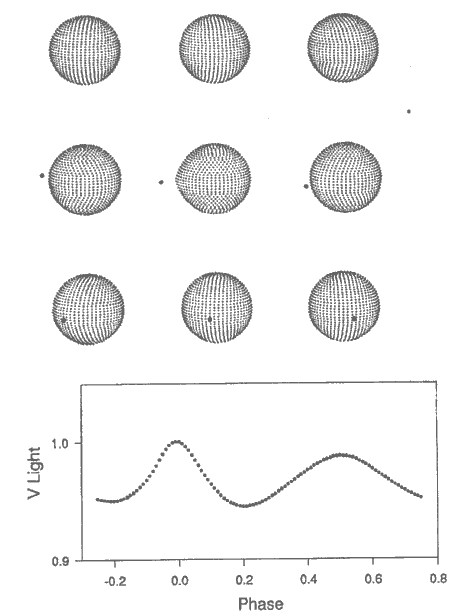
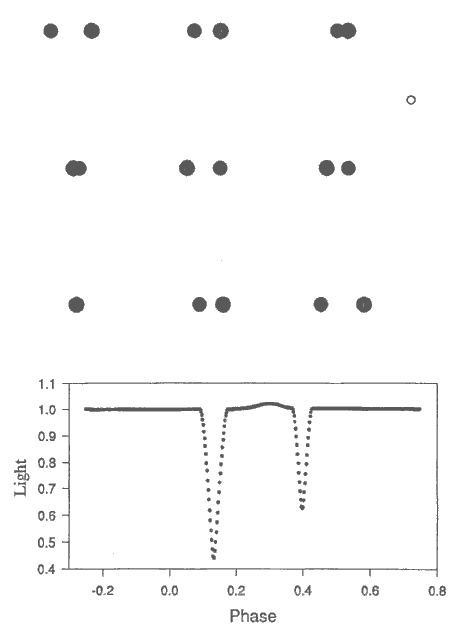| FIGURE 5. V 1647 Sagittarii shows a variety of eccentric orbit effects, including unequal eclipse widths and separations, and a reflection peak near periastron (about phase 0.3). The light curve was computed at 0.2 microns. The small circle in the upper right margin represents the Sun on the same scale. |
The list below does not include all useful rules, as you may want to come up with some of your own, but here are some major ones:
Lack of exactness in these rules is not important because we have programs for accurate computing. What the interpreter needs is a general idea of how light curves relate to binary stars. For example, suppose a screen plot shows the eclipse widths to be less for the model than for some real star. According to rule 5 the sum of the relative radii is too small in the model, so the sum needs to be increased, assuming the inclination is about right (rule 7). Whether this is done by increasing one radius or both must be considered in the context of several other rules.
Now suppose you have applied the above rules and perhaps a few of your own to real observations, preferably at two or more effective wavelengths. When you have a visibly good match between the computed and observed light curves, you already will have achieved more than typically was done 30 years ago in professional work. The models then were far less realistic than the modern one you will have, and the fitting process was the same as yours, that of trial and error. However you can go further with a least squares fitting program.
In overview, the purpose of any such program is to find a set of parameter values which produces best agreement between theory and observation in the least squares sense (see above). There are several ways of going about this, such as Differential Corrections (DC), Steepest Descent, the Simplex algorithm, and the Marquardt algorithm, all of which have come from the mathematics literature. The various modelers have their preferences among these methods and occasionally switch. At present, for example, Hill and Rucinski use Marquardt, Kallrath Simplex, Linnell both DC and Simplex, Wilson DC, and Wood DC. With help from program documentation, it should be possible to apply these methods without getting very deeply into their mathematical foundations. However it would be good to understand something of how they work, so a survey of the essential ideas of the more commonly used fitting algorithms will now be outlined.
All of the procedures are iterative. Again, the quantitative measure of fit is the Sum of Squares of weighted residuals, which we symbolize by SS. DC looks at how the observable quantity (e.g. binary system light) changes with variations in each parameter, and also tries to take into account the interactions among parameters (correlations). DC takes a given provisional solution and calculates local partial derivatives, of light with respect to each parameter, to see which way to move so as to make the SS smaller. Steepest Descent looks at a different kind of derivative, that of SS with respect to each parameter, and does not attempt to deal with correlations. This can be a disadvantage, but also can keep it out of trouble, since the correlations may not be computed correctly in a highly non-linear problem. The Marquardt (1963) algorithm essentially looks at both the DC and Steepest Descent results and chooses a safe compromise. Simplex does not calculate partial derivatives or local slopes, but consists of a set of rules for taking safe steps which usually head downward in SS, including rules to recover if SS should increase. A more complete discussion is in Wilson (1994).
Before trying for a least squares solution, think hard about your trial and error solution. Consider whether there can be another set of parameter values, perhaps quite a bit removed from the set you have now, which might fit about as well or better. If so, you have encountered the infamous "local minimum" problem, which can afflict any of the methods used to reach a minimum. Think of rolling countryside, with adjacent lakes at different levels. The water in the higher lake would flow into the lower one if they were connected, but since they are not the lakes remain separate. Similarly, a solution in "parameter space" can be trapped at a local minimum, which is not the deepest minimum and therefore not the preferred solution.
On the practical side, there are issues of whether or not the iteration process should be automated and how a person should become involved in the iterations (if at all), how to compute the partial derivatives, when to stop the iterations, and when to sense that something just is not right, even though the solution algorithm seems to have found a minimum of SS. All of this is in the realm of experience and common sense, but the following overview may be helpful. First, one always should compare computed and observed light curves, inspect the graphs, and think about what they mean. Do not accept numbers which just "fall out of the machine" without critical evaluation. While many professionals favor automatic iteration, the author advocates interactive branching (Wilson 1988), in which each iteration is examined for reasonableness and the set of adjusted parameters may be changed occasionally. The advantage is that one can draw on the experience of seeing how the solution is proceeding when adjusting parameters
Another point concerns the computation of the partial derivatives in DC. Most of these derivatives are computed numerically by varying a parameter a little and computing the resultant change in system brightness. How much should the parameter be varied? Guidelines may be found in the documentation for the various programs (e.g. Wilson 1992), but something like a one percent increment should be about right for many parameters. What about when to stop? Rarely will corrections be essentially zero, because of the finite difference arithmetic, correlations, and several other realistic problems. Several persons have made the point that iterations should stop only when the solution no longer drifts systematically in any direction, but jiggles around within a small region of parameter space (e.g. Linnell 1989). The WD program can solve multi- bandpass (e.g. U,B,V) light curves and radial velocity curves simultaneously, and this advantage should be utilized in most circumstances, although a proper discussion would lead us somewhat afield. This capability is covered in Wilson (1979; 1992; 1994)
Finally there is the matter of how can one recognize a seriously inadequate solution and take corrective measures. Astrophysically implausible results should stimulate thorough consideration of possible alternatives, such as another morphology or perhaps just another starting point for the iterations. Keep in mind, of course, that the implausible can sometimes be both correct and more interesting than the expected. Poor solutions often are revealed by sections of the light curve in which the computed and observed curves disagree systematically. Sometimes that can follow from transient behavior of the real binary or from some inadequacy of the model, but it also can happen at a local minimum in SS which is not the deepest minimum. If the latter is suspected, start from several previously untried points and try again. Make screen plots to compare your computed curves with the observations and try to understand as much as you can about plausible reasons for any systematic deviations. Discuss your developing results with anyone who will listen. Of course the final plot will be in your publication, and will be the main way for readers to judge your success, so fit as well as you can, and understand as well as you can.
Your experiments will help you to recognize wrong and misleading explanations and diagrams. For example, several books illustrate the internal structure of an overcontact binary by a figure showing dark color up to the Roche lobes and light shading between the lobes and the surface. A reasonable person would infer a sharp drop in density at the lobe surface, like the air over the ocean, which is not at all the case. The part of the envelope which lies above the Roche lobes is an ordinary extension of the underlying envelope.
One text introduces eclipsing binaries with this statement: "If the orbit of a spectroscopic binary is almost exactly edge-on to us, one star will pass directly in front of the other, producing an eclipse". This is not formally incorrect, but is certainly misleading. Inclinations of 70° and lower, which is far from exactly edge-on, can give eclipses in many realistic and commonly encountered situations.
In several books, explanations of what can be found from eclipse durations show lack of understanding of the rules of Section III. Simplification can be useful in beginning explanations, but should not include assertions which are actually wrong. Along this line, one book states that "... the relative depths of the two eclipses are related to the ratio of the stars' temperatures". Yes, there is a connection with temperature but it is not just in the temperature ratio. This is almost like saying that the relative rebounding ability of two basketball players is related to their height ratio (well, perhaps not quite that bad).
Loose thinking is shown by failure to distinguish between light per unit area and total light, and between bolometric (over all wavelengths) light and light in a spectral bandpass. Diagrams often lack scales and units, which prevents inference of anything quantitative. Illustrated light curves may be incompatible with pictured binaries, even in the roughest approximation. It is easy to print real observations or computed curves, yet most books show only schematic renditions. Tidally distorted stars may be shown as spheres. The list could be much longer and more detailed, but the reader may wish to identify the various defects as an educational experience. So indeed read text books, but not at the start. First make thought experiments and graphics experiments. Then, facing a library table covered with texts opened to "binary stars", ask how you would have written them.